Andre kunder købte også..

Der har været mange som har efterspurgt nogle mere tekniske artikler, og jeg kan godt forstå det - jeg har også selv opsøgt at forstå machine learning ned i mindste detalje.

Derfor vil jeg i denne artikel skrive en slags fortsættelse til Mersalg via produktforslag artiklen. Der er rigtig mange forskellige måder man kan implementere det på, men jeg vil heri beskrive nogle gode teknikker som har bevist deres værd i flere forskellige sammenhænge.

Overordnet så falder de fleste teknikker til produkt-forslag ind under kategorien "Collaborative Filtering". At det er "collaborative" kommer af at når man vil anbefale produkter til en specifik kunde, så gør man det typisk ved at kigge på data fra en masse andre kunder, og på den måde kan man sige at de andre kunders data arbejder sammen for at give dig produktforslag. Typisk vil man på den måde ende med et meget stort antal produkter man kan foreslå, og man ønsker derfor at vælge de bedste ud så det ikke bliver et for overvældende antal muligheder - derfor "filtering".

Matematisk udtrykker man det som en (ofte kæmpe stor) matrix der har produkter på den ene akse og kunder eller andre produkter på den anden.

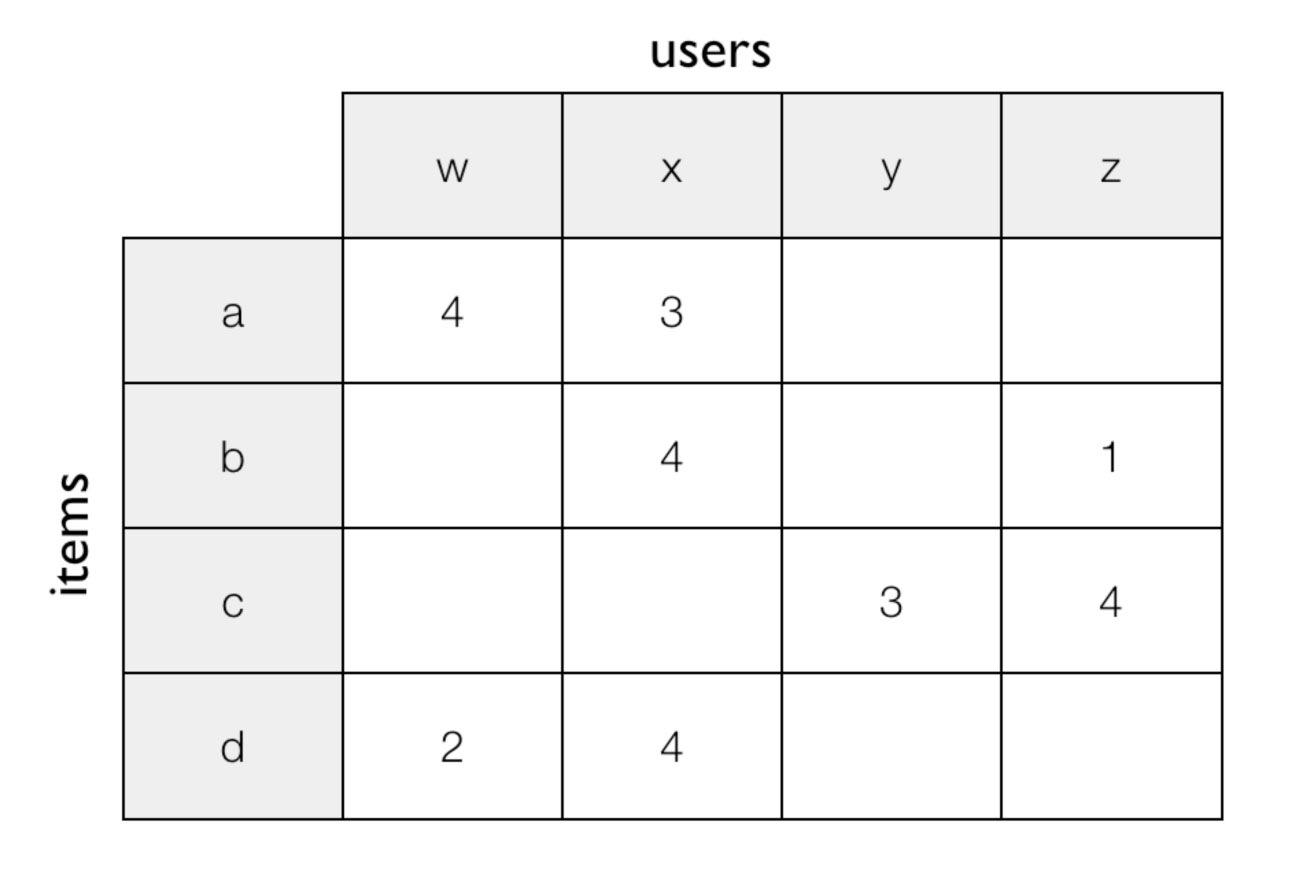
Den simpleste teknik er at opsamle købs-statistik og i matricen notere hver gang et produkt bliver købt sammen med et andet produkt (man har produkter på begge akser), og så direkte bruge det som en score for hvor ofte produkt A og produkt B købes sammen. Hvis en kunde besøger en side med produkt A - så tager man enten den række eller den kolonne i matricen som tilhører A og så finder de celler med de højeste scores og anbefaler de produkter.

I praksis giver det dog ret kedelige forslag. Hvis man f.eks. anbefaler film, så er der rigtig mange folk som har set filmen Titanic, og man vil derfor ende med at foreslå Titanic til stort set alle som systemet ikke allerede ved har set filmen. I de fleste tilfælde vil folk allerede have set filmen hvis de mente at have interesse for den, så på den måde ender man med at "spilde" en masse forslag.

En rigtig god teknik til at give bedre forslag er at bruge den teknik som hedder Pointwise Mutual Information. Til den bruger man præcis den samme matrix hvor man har talt op hvor ofte 2 produkter bliver købt sammen, men ved siden af den så har man også en liste med hvor ofte hvert produkt bliver købt i det hele taget. Det man så ønsker at opnå er at kompensere for produkter der bare generelt er meget populære og så kun anbefale produkter der bliver købt sammen i overraskende høj grad.

Det er her at jeg bliver nødt til at introducere lidt matematik. Matematisk så udtrykker man ofte "hvor ofte noget bliver købt" som hvad er sandsynligheden for at produkt x bliver købt og man skriver det som p(x). På samme vis kan man skrive p(x, y) for at indikere hvor ofte to produkter bliver købt sammen. PMI er så defineret som følgende formel:

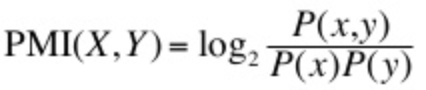
I sandsynlighedsteori er p(x) * p(y) hvor ofte 2 ting forventes at ske samtidigt hvis de er uafhængige af hinanden. Så basalt set gør PMI det at tallet for hvor ofte 2 produkter bliver købt sammen bliver divideret med hvor ofte man ville forvente at de blev købt sammen ud fra ren statistik. Derfor betyder en brøk over 1.0 at to produkter bliver købt overraskende ofte sammen og hvis den er under 1.0 så bliver de købt overraskende sjældent sammen. Traditionelt er der så en logaritmisk faktor også, som bare sørger for at gøre tallene mindre følsomme for store udsving som følge af støj i data.

Med PMI vil man ofte få meget mere interessante produktforslag fordi det netop er de produkter som hænger særligt meget sammen i folks købsmønstre der bliver anbefalet. Det kan være et batteridrevet stykke legetøj og en pakke batterier, eller det kan være koldskål og kammerjunkere.

PMI er godt til tilfælde hvor man ikke ved så meget om en potentiel kunde, man ved måske kun at kunden lige nu kigger på et specifikt produkt. Hvis man yderligere har historiske data på kunden, så kan man forsøge at være mere avanceret. Hvis man f.eks. har data på et stort antal kunder omkring alle de produkter de har købt tidligere, så kan man ydnytte det via en simpel ide: Hvis en særlig gruppe af andre kunder har købt mange af de samme produkter som dig, så er det måske fordi du som kunde i dine præferencer minder om de kunder som allerede er i den gruppe. Det vil man så bruge til at anbefale produkter som dem i gruppen godt kan lide, men som du endnu ikke har købt.

I praksis er en god teknik til sådan en situation at lave matrix factorization. Ligesom med PMI så udtrykker man sit problem som en stor matrix, men i stedet for at matricen indeholder hvor ofte et produkt er købt sammen med et andet produkt - så har den produkter på den ene akse, kunder på den anden og hver celle indikerer om en kunde har købt eller ej (eller alternativt hvor mange stjerner kunden har anmeldt produktet til). Sådan en matrix vil være meget stor og typisk vil der ikke være ret mange celler som faktisk er udfyldt - man kalder det en sparse matrix.

Fordi der ikke er ret mange celler udfyldt, så er det nærliggende at spørge sig selv om man måske kan lave en slags tilnærmelse der bibeholder købsmønstre. Det er det man gør med matrix factorization. I stedet for at arbejde på den fulde matrix (lad os kalde den A) så forsøger man at finde 2 mindre matricer (kaldet W og H) der når man ganger dem sammen ender med at tilnærme A:

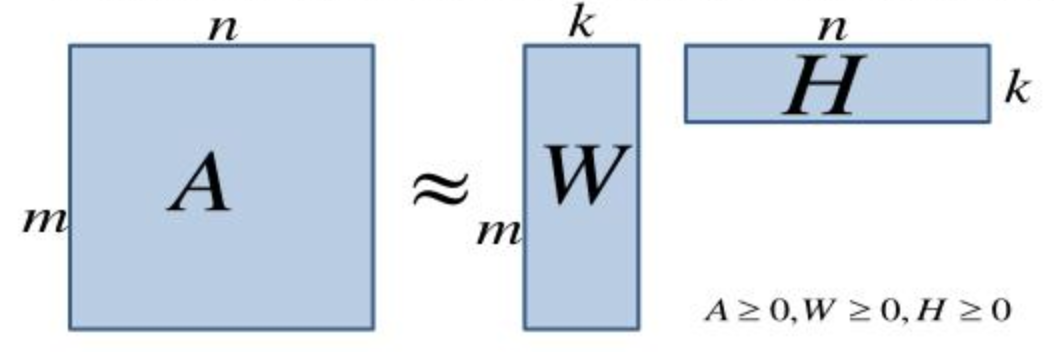
At finde disse 2 matricer er en rimeligt standard operation som man i mange programmeringssprog kan finde biblioteker der tilbyder. Hvis man programmerer i Python er der f.eks. sklearn.decomposition.NMF til at gøre det for sig. De virker ved at man bestemmer hvor mange henholdsvis kolonner og rækker man ønsker i W og H og så får man den bedste tilnærmelse ud fra de parametre.

Det interessante er at i praksis så kan man betragte kollonner og rækker i W og H som såkaldte latente faktorer for henholdsvis kunder og produkter - man ender simpelthen med en vector af tal for hver kunde og for hvert produkt og når man ganger de vektorer sammen får man direkte et udtryk for hvor godt produktet passer til kunden. På den måde kan man udfylde hele matricen, også de kombinationer som man endnu ikke har data for!

Samtidigt betyder det også at kunder der har vektorer som ligner hinanden også ligner hinanden i deres produkt-præferencer - så man har nu pludseligt mulighed for at udlede et tal for hvor meget 2 kunder eller 2 produkter ligner hinanden og kan f.eks. begynde at bruge clustering teknikker til at visualisere hvordan ens kunder deler sig op i forskellige grupperinger.

Somme tider vil man gerne udnytte endnu flere data, det er f.eks. meget almindeligt at man har en masse ekstra data omkring produkterne. Eller det kan også være at kunderne er aktive på en social platform og man ønsker at bruge de data (indlæg, likes, med mere) til at beskrive kunderne mere præcist. I sådanne tilfælde er man nødt til at lave en mere skræddersyet machine learning model, og det vil typisk være en model som gør brug af deep learning teknikker. Det er også i de tilfælde at det giver særligt god mening at hyre et firma som MachineReady da vi allerede har stor erfaring med at lave den slags mere avancerede modeller.

Jeg håber det har været spændende at læse om nogle af de gode teknikker til at lave produkt-forslag. Det er et område som ofte direkte påvirker en virksomheds bundlinie og derved er det også et godt sted at starte med at introducere machine learning i en virksomhed - man kan direkte måle på om man får flere salg eller ej.